Quantized Light and The Photoelectric Effect
In the explore section, you measured the effect that different colours and intensities of light had on a photocathode. What you were measuring was the build-up of charge on a capacitor, due to electrons that were ejected from the photocathode as the light struck it. Three features in the data you collected should have stood out:
- Some colours produced no charge
- Some colours produced higher voltages
- The speed of charge build-up varied with the intensity of the light
Below we will try to explain each of these observations in the framework of a particle theory of light. The key feature of this theory is that light can be thought of as a tiny packet of energy that is localized in space (and not spread-out like a wave). The energy of these packets (called ‘photons’) depends on the frequency of the light. Higher frequency photons have higher energy. The energy \(E\) can be calculated from the frequency \(\nu\), using the Planck Relation:
where \(h\) is Planck’s constant, which is equal to \(6.626 \times 10^{-34} \mathrm{m^2 kg \ s^{-1}}\). (Remember, wavelength and frequency are related by \(λν=c\). Higher frequency means lower wavelength.)
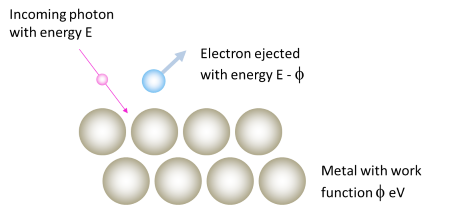
Electrons ejected from the surface do not have all of the photon’s energy – some of it (the work function) is used up just getting the electron out of the metal.
Why do some colours produce no electrons?
The photoelectric effect is all about kicking electrons out of metals, using light. However, it takes a certain amount of energy just to get an electron to the point where it can leave the surface of the metal. If this wasn’t true, and electrons did not require a certain amount of initial energy, then they would be free to leave the metal at any time. We know that this does not occur, and so we conclude that an electron must have a certain minimum amount of energy before it can leave the metal.
This minimum (or threshold) energy is called the work function of the metal. We measure it in units of electron volts (eV), and give it the symbol \(\phi\). If an electron is ejected by a photon of energy \(E\), then it will leave the metal with energy \(E-\phi\), because the energy of the work function was lost in getting the electron out of the metal. The table below lists the work functions for some common metals.
So why do some colours eject no electrons? Because the photons of that colour do not have the minimum amount of energy required to overcome the work function of the metal. For example, suppose we were using blue light, with a frequency of \(\nu = 6.362 \times 10^{14} s^{-1}\). The Planck relation we saw above says that photons of a certain frequency (which means light of a certain colour) will have energy equal to:
\begin{aligned}E & = h\nu \\
& = 6.626 \times 10^{-34} \times 6.362 \times 10^{14} \\
& = 42.15 \times 10^{-20} \ \mathrm{Joules} \\
& = 2.635 \ \mathrm{eV}
\end{aligned}
\)
Looking at the table below, from which metals could we eject electrons using this colour of light?
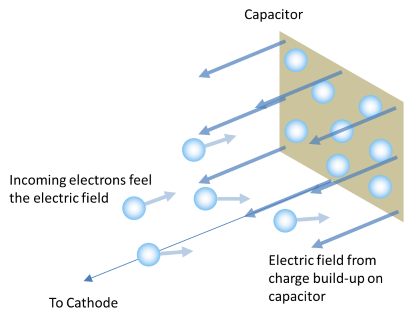
As electrons build up on the capacitor, the electric field they produce starts to repel incoming electrons.
Why does the maximum voltage depend on the colour of the light?
We know from the Planck relation that photons of different colours have different energies. We also know that in order to eject any electrons at all, the energy of those photons must be greater than the work function of the metal we are trying to eject electrons from. If our photons do have enough energy, the ejected electrons will leave the surface of the metal with energy \(E-\phi\).
When the electrons are ejected, the fly off the surface and are collected by a capacitor. As the number of electrons on the capacitor increases, the electric field from all these electrons starts to repel the new electrons that are continuously being ejected from the metal. This repelling electric field slows down the approaching electrons. When enough electrons are on the capacitor, and the repelling field has grown strong enough, eventually the approaching electrons will be slowed down so much that they stop before they reach the capacitor (and then they will be turned around and accelerated back toward the metal!).
So what does this have to do with the photon colour? Well, since photons of shorter wavelength (toward the blue end of the spectrum) have greater energy (higher frequency), they will eject electrons with more initial energy than photons toward the red end of the spectrum. Having a greater energy when they leave the surface of the metal, it will take a stronger electric field to stop them reaching the capacitor. So the capacitor will need to collect more electrons (which means it will acquire a larger voltage) in order to repel photons from the blue end of the spectrum than it will to repel those from the red end. The result is that shorter wavelengths of light (higher frequencies and greater energies) will give the capacitor a greater charge than will longer wavelengths.
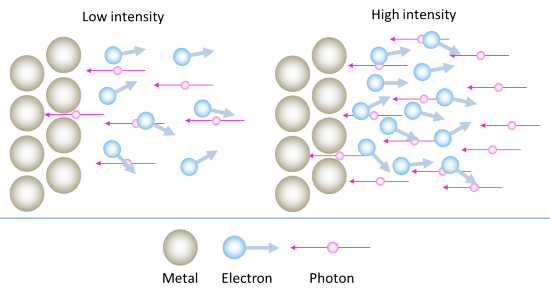
How does light intensity affect the charging time?
This one is easy. In the particle model of light, a higher intensity (brighter light) means more photons. Technically, we should say that a higher intensity corresponds to a greater number of photons passing through a given area in a given amount of time.
Remember that every photon is a packet of energy, and each packet of energy can eject an electron. If we have more photons hitting the surface of the metal every second, as we would if we increase the intensity of the light, then we will be ejecting more electrons every second. Note that each of these electrons still leaves the surface with about the same energy as before – we have not changed the wavelength of the light, only its intensity.
With more electrons leaving the surface every second, the capacitor will be collecting them at a faster rate, and will therefore build up its charge more quickly. Thus the graph of capacitor voltage versus time will reach its plateau more quickly. So we think of it like this:
- Low intensity \(\rightarrow\) few electrons ejected per second \(\rightarrow\) slow build-up of charge on capacitor
- High intensity \(\rightarrow\) many electrons ejected per second \(\rightarrow\) rapid build-up of charge on capacitor